地図の制作
地図を作ることを「地図調製」といいます。地図調製は、大きく分類すると1)地図デザイン〈企画・設計〉、2)データ編集、3)印刷、の3工程に分けられますが、その作業は大変複雑で、とくに1)の企画と2)の編集では、熟練した技術者の経験と知識が不可欠といえます。弊社は、国土交通省国土地理院の基本図の作成をはじめ、地方自治体の行政用地図、民間向けの地図出版まで、数多くの実績を持つことを一つの誇りとしています。
多種多様な地図を目的に合わせて制作いたします
教育用 各種日本地図
▲日本地図
▲イラストマップ
各種世界地図
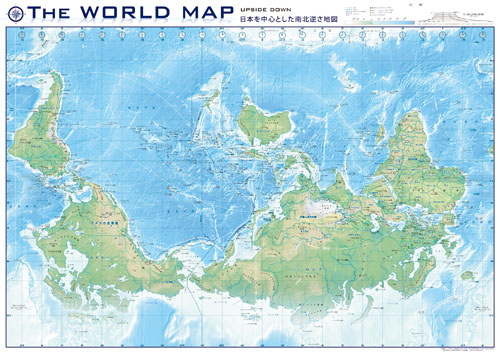
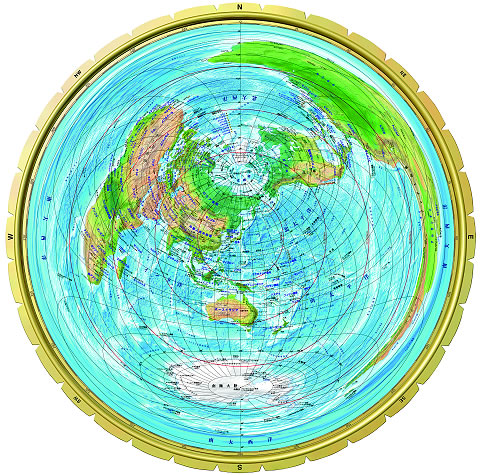
▲南北逆の世界地図
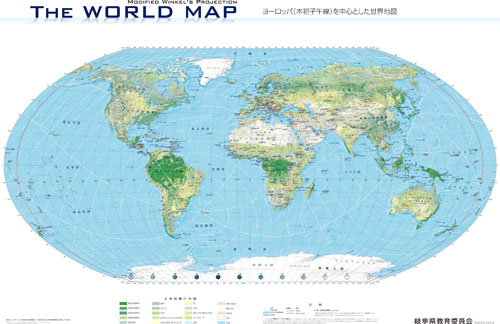
▲ヨーロッパ(経度0°)が中心の世界地図
主題図
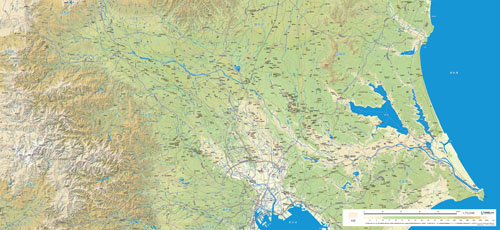
▲博物館向け大判地図
目的の地図を制作する上で最も重視すべきことは、単にきれいな線でトレースしたきれいな地図を作ることではなく、いかに判り易く使い易い地図を作れるかという点です。そのために重要になるのは編集技術です。熟練した技術者のノウハウと、最新のコンピューター技術の融合により、21世紀の新しい地図づくりを目指しています。
コンピューター技術を駆使したデジタル地図
地図投影の手法をはじめ、色・レイアウトなどのデザイン、また地図上に載せる情報のカスタマイズや、GIS上で作成された地図データから紙地図を作成するなど、お客様のさまざまなご要望にお応えいたします。
距離圏、方位線が組み込まれたメルカトル図法
〈第4回優秀地図技術者表彰、国土地理院長賞受賞作品「THE WORLD MAP青い地球」〉
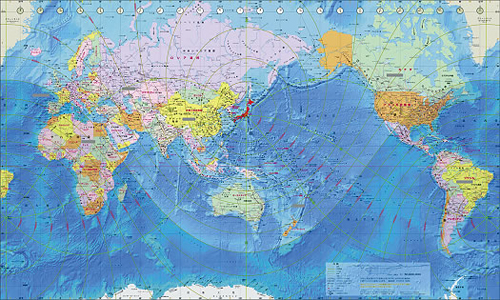
東京を中心とした正距方位図法(Azimuthal Equidistant Projection)によるユニークな世界地図
デジタルデバイスで地図を使用する
現在スマートフォンやタブレットなど様々なデジタルデバイスで利用されているデジタル地図は、単に”絵”としての地図を表示するだけではなく、検索や集計・分析などGIS上で活用できるようにするため「地図データベース」の作成が不可欠となります。弊社は、各種数値地図(国土交通省国土地理院)のデータ作成をはじめ、さまざまな分野で活用されている道路地図データベースの作成まで、幅広く対応しています。また国土空間データ基盤の整備事業にいち早く取り組み、官民共同の研究活動を通じて地図データベースの作成・運用・更新のための技術開発に積極的に取り組んでいます。
デジタル地図データベースの完成まで

立体的に見える地図の表現方法
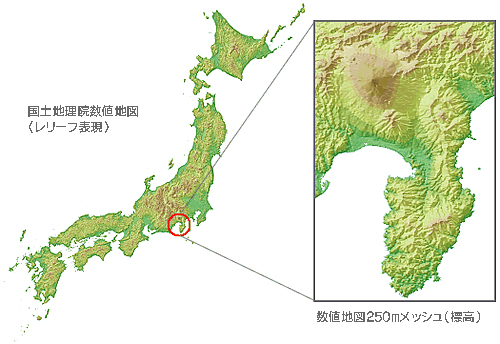
地図を立体的に表現する方法として、等高線をもとに高さで色分けする方法や、山の斜面にシェーディング(レリーフ/陰影)をつける方法、鳥瞰図(鳥が空から地上を眺めた時のような立体的な図)化する方法などがあります。こうした高度な3次元地図も、コンピューター技術の活用により、高精度且つ短期間で作成することができます。
美しい3次元地図
標高データを用いたレリーフ表現
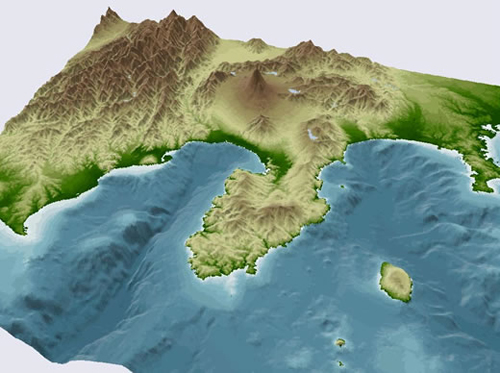
鳥瞰図
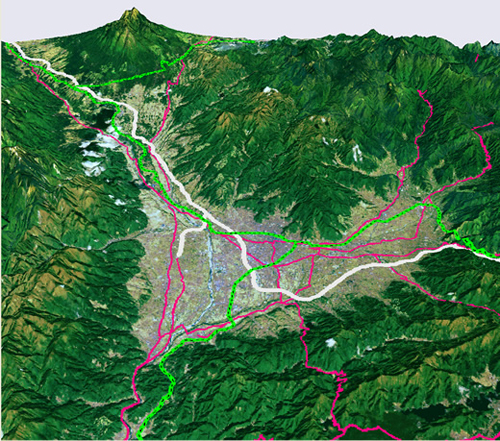
白:高速道路 ピンク:国道 緑:鉄道
地図づくりと「投影」
さまざまな「投影」
丸い地球を”地図”という平面上にどう表現するか、それは地図づくりに携わる者にとって永遠の課題です。同じ世界地図でも、メルカトル図法、モルワイデ図法、断裂ホモロサイン図法、アダムス図法など、どの投影法を選ぶかによって全く違う形の地図が出来上がります。いずれの投影法も、ある一つの面に対しては距離・方位・面積を正確に表現できますが、別の面では必ず歪みが生じます。つまり、すべての面を正確に表現できる投影法が存在しない以上、地図の目的によって投影法を選んで使用しなくてはならないのです。それはすなわち、地図を制作する人の知識やセンス、そして”技”の見せ所でもあります。
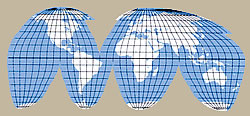
▲断裂ホモロサイン図法
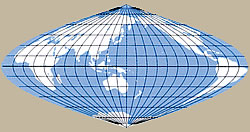
▲サンソン図法
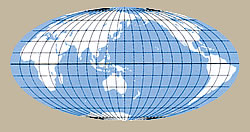
▲モルワイデ図法
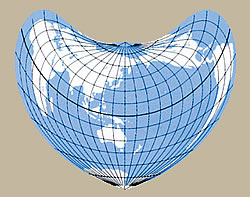
▲ボンヌ図法
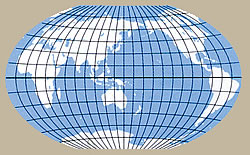
▲ビンケル図法
地図投影の特性と利用目的
地図を作成するには、まず利用目的とその目的に合った縮尺方法、使用する範囲などを決め、それに応じて適切な投影法を選ぶ必要があります。またそれを利用する人が誤った読み取り方をしなように、それぞれの投影法の特性を十分考慮した読み易い地図に仕上げなくてはなりません。以下は、主な投影法の特性を、3つの視点(性質/適用地図/一般用途)で分類・整理したものです。地図の新規作成を検討される時などの参考にしてください。
性質
適用地図
一般用途
性質
| 〈投影〉 | 正角 | 正積 | 正距 | 正方位 | 投射 | 折衷 | 航程 線直 |
|---|---|---|---|---|---|---|---|
| 地球儀(球) | ◎ | ◎ | ◎ | ◎ | × | × | × |
| メルカトル(円筒) | ◎ | × | × | ▲ | × | × | ◎ |
| 横メルカトル | ◎ | × | × | × | × | × | × |
| 斜軸メルカトル | ◎ | × | × | × | × | × | × |
| スペース斜軸メルカトル | ◎ | × | × | × | × | × | × |
| ミラー | × | × | × | × | × | ◎ | × |
| ロビンソン(擬円筒) | × | × | × | × | × | ◎ | × |
| サンソン | × | ◎ | ▲ | × | × | × | × |
| 正射(方位) | × | × | × | ▲ | ◎ | × | × |
| 平射 | ◎ | × | × | ▲ | ◎ | × | × |
| 心射 | × | × | × | ▲ | ◎ | × | × |
| 正距方位 | × | × | ▲ | ▲ | × | × | × |
| 正積方位 | × | ◎ | × | ▲ | × | × | × |
| アルベルス(円錐) | × | ◎ | × | × | × | × | × |
| 正角円錐 | ◎ | × | × | ▲ | × | × | × |
| 正距円錐 | × | × | ▲ | × | × | × | × |
| 多円錐 | × | × | ▲ | × | × | ◎ | × |
| 2極斜軸正角円錐 | ◎ | × | × | × | × | × | × |
| ◎:該当する ▲:一部該当する ×:あまり当てはまらない | |||||||
適用地図
| 〈投影〉 | 全世界 | 半球 | 大陸・大洋 | 地方・海岸 | 中縮尺 | 大縮尺 |
|---|---|---|---|---|---|---|
| 地球儀(球) | ◎ | × | × | × | × | × |
| メルカトル(円筒) | ▲ | × | × | ◎ | × | × |
| 横メルカトル | × | × | ◎ | ◎ | ◎ | ◎ |
| 斜軸メルカトル | × | × | ◎ | ◎ | ◎ | ◎ |
| スペース斜軸メルカトル | × | × | × | × | × | ◎ |
| ミラー | ◎ | × | × | × | × | × |
| ロビンソン(擬円筒) | ◎ | × | × | × | × | × |
| サンソン | ◎ | × | ◎ | × | × | × |
| 正射(方位) | × | ▲ | × | × | × | × |
| 平射 | × | ◎ | ◎ | ◎ | ◎ | ◎ |
| 心射 | × | × | × | ▲ | ◎ | × |
| 正距方位 | ▲ | ◎ | ◎ | ◎ | × | ▲ |
| 正積方位 | × | ◎ | ◎ | ◎ | × | × |
| アルベルス(円錐) | × | × | ◎ | ◎ | ◎ | × |
| 正角円錐 | × | × | ◎ | ◎ | ◎ | ◎ |
| 正距円錐 | × | × | ◎ | ◎ | × | × |
| 多円錐 | × | × | × | × | ▲ | ▲ |
| 2極斜軸正角円錐 | × | × | ◎ | × | × | × |
| ◎:該当する ▲:一部該当する ×:あまり当てはまらない | ||||||
一般用途
| 〈投影〉 | 地球図 | 地質図 | 主題図 | 説明図 | 航法図 |
|---|---|---|---|---|---|
| 地球儀(球) | × | × | ◎ | ◎ | × |
| メルカトル(円筒) | ◎ | ◎ | × | × | ◎ |
| 横メルカトル | ◎ | ◎ | × | × | × |
| 斜軸メルカトル | ◎ | × | × | × | × |
| スペース斜軸メルカトル | ◎ | × | × | × | × |
| ミラー | × | × | ◎ | × | × |
| ロビンソン(擬円筒) | × | × | ◎ | ◎ | × |
| サンソン | × | × | ◎ | × | × |
| 正射(方位) | × | × | × | × | × |
| 平射 | ◎ | ◎ | × | × | ◎ |
| 心射 | × | × | × | ◎ | ◎ |
| 正距方位 | ◎ | × | × | × | × |
| 正積方位 | × | × | ◎ | ◎ | × |
| アルベルス(円錐) | × | × | ◎ | ◎ | × |
| 正角円錐 | ◎ | ◎ | × | ◎ | ◎ |
| 正距円錐 | × | × | × | × | × |
| 多円錐 | ◎ | × | × | × | × |
| 2極斜軸正角円錐 | × | ◎ | × | × | × |
| ◎:該当する ▲:一部該当する ×:あまり当てはまらない | |||||
